题目:
Given a linked list, return the node where the cycle begins. If there is no cycle, return
null.Follow up:
Can you solve it without using extra space?
分析:
检查链表是否有回路。如果有回路,则返回回路的起始节点;如果没有,则返回null。
基本思路还是使用Floyd判圈算法。指针hare每次向后移动2个节点,指针tortoise每次向后移动1个节点。如果hare最终指向尾节点则该链表无回路。否则,该链表有回路。(详见《LeetCode #141 Linked List Cycle》)
现在我们已经知道了链表有没有回路,但是如何在不使用额外空间并且不修改原链表的基础上获得回路的起始节点呢?这需要一些数学推导:
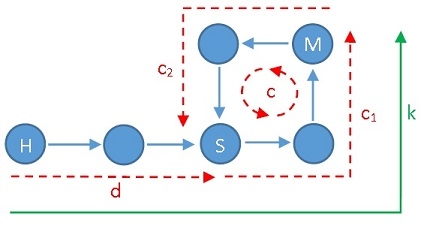
设链表起始节点为H,回路起始节点为S,两指针第一次相遇节点为M。
设回路的长度为c,S到M的距离为c1,M到S的距离为c2。
设H到S的距离为d。
设hare每次移动2,tortoise每次移动1。移动k次后两者相遇。不难发现,H到M的距离为k。
为了便于理解,请参考下图: